Bitcoin cai abaixo de US$ 114 mil em meio à cautela pré-Jackson Hole
Olá, pessoal. Neste artigo, desmistifico o Critério de Kelly e explico precisamente qual o seu contexto, para que serve e se ele pode ser utilizado como estratégia em apostas esportivas e em investimentos. Costumo receber perguntas a respeito do que seria a tal “estratégia de Kelly”. É muito comum, via rede social ou mesmo pessoalmente, me fazerem a seguinte pergunta:
“Professor, ouvi falar de uma tal estratégia de Kelly para investimentos: como ela funciona?”
Mais recentemente, com o avanço intenso das casas de apostas esportivas (as “bets”), a mesma pergunta começou a me ser feita neste contexto também. Pois bem, resolvi dar minha resposta completa e final para estas questões escrevendo este artigo. Nele, desmistificarei a tal “estratégia de Kelly” (que, na verdade, é conhecido como Critério de Kelly), explicando qual o seu contexto de aplicação e quais os limites de validade no que diz respeito a apostas esportivas e investimentos.
Acho bacana começar dizendo que o critério foi desenvolvido por John Larry Kelly Jr. em seu artigo acadêmico “A New Interpretation of Information Rate”, publicado em 1956 no Bell System Technical Journal. Para quem quiser ler o artigo, basta procurar online porque ele é facilmente encontrado.
QUAL O CONTEXTO DE VALIDADE DO CRITÉRIO DE KELLY?
Imagine que alguém lhe ofereça o seguinte jogo e você pode jogá-lo quantas vezes quiser, desde, claro, que tenha dinheiro para isso: uma moeda honesta é lançada e se der cara, você recebe o triplo do que apostou; se der coroa, você perde o montante apostado. Note que este jogo é bom e devemos entrar porque a expectativa é de ganho, tendo em vista que há 50% de chances de vitória e 50% de chances de derrota, com a diferença de que na vitória você recebe o triplo do que tem de prejuízo no caso de derrota. Claro que você pode perder dinheiro neste jogo, pois afinal de contas, a moeda pode dar coroa! Mas quando você tem a possibilidade de jogar quantas vezes quiser, a Lei dos Grandes Números dissipa o risco e faz com que, em média, você ganhe a metade do montante apostado a cada rodada jogada. Por exemplo, se você apostar R$ 100,00, sua expectativa de faturamento em uma rodada deste jogo é de R$ 150,00, ou seja, R$ 50,00 de lucro:
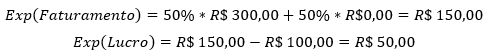
Em outras palavras, se você jogar por muitas vezes esse jogo, digamos que sempre apostando R$ 100,00, você tenderá a lucrar R$ 50,00 vezes o número de rodadas jogadas. A grande questão aqui é: quanto você deve apostar a cada rodada? Essa pergunta parece trivial, mas definitivamente não é. Todos temos recursos finitos e, sem perder a generalidade, suponha que você tenha R$ 10.000,00 ao todo para apostar neste jogo (o valor mencionado é meramente ilustrativo: adapte-o para a sua realidade). Uma decisão totalmente ingênua é investir tudo que você tem logo na primeira rodada, mas aí, claramente, se der coroa, você perde tudo e não tem mais dinheiro para fazer novas apostas. Aí você pensa: “ah, entendi; então vou apostar 50% apenas e manter 50% como gordura para a próxima rodada”. Certo, mas se der coroa na primeira e na segunda rodadas, você acaba falido e fora do jogo! Note: há 25% de chances disso acontecer.
Não importa que fração você escolha para jogar, se você seguir apostando o mesmo montante, sempre haverá uma chance de você ir à falência e não se beneficiar de um jogo bom para você (no sentido de que ele te dá mais chances de ganhos do que de perdas). Com isso, apostar sempre o mesmo montante é uma estratégia que pode te levar à perda total do valor disponível para o jogo.
Qual a solução então? Apostar sempre uma fração (ou um percentual, se você preferir) do que você tem disponível. Desta maneira, como matematicamente uma fração não-nula de qualquer quantia jamais te deixará zerado, você jamais irá à falência. Mas, aí a pergunta que se impõe é: qual deve ser essa fração ideal? Porque seria 50% e não 40% ou 60%? Bom, é precisamente esse o problema que Kelly resolveu.
QUAL A SOLUÇÃO IDEAL, OU SEJA, QUAL O PERCENTUAL IDEAL QUE SEMPRE DEVERÁ SER APOSTADO NESTE JOGO?
Aqui é importante compreender o que queremos dizer com “ideal”. Ideal aqui representa dizer que percentual maximiza a minha expectativa de riqueza ao final de várias rodadas deste jogo. Pois bem, nosso adorável e brilhante Kelly resolveu esse problema e eis a fórmula matemática conhecida como Critério de Kelly que resolve a questão (nota: a fórmula abaixo é uma versão simplificada da fórmula generalizada, mas que serve perfeitamente para os propósitos deste artigo):
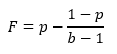
Na fórmula acima, F é a fração do montante total disponível para aquele jogo que deve ser apostada a cada rodada; p é a probabilidade de vitória e b, o montante recebido a cada um real apostado em caso de vitória (e que será perdido totalmente em caso de derrota, que tem probabilidade 1 – p).
Para ilustrar o uso do Critério de Kelly, no nosso exemplo, temos p = 0,50 (50% de dar cara e você ganhar) e b = 3 (para cada R$ 1,00 apostado, seu ganho será de R$ 3,00). Com isso, você deverá sempre apostar 25% do que você tiver disponível para aquele jogo (veja a seguir a fórmula acima aplicada):
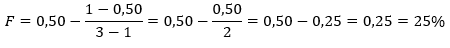
O que o resultado acima nos diz é o seguinte: você pode ter qualquer estratégia ao longo das rodadas do jogo apresentado aqui, mas aquela que maximiza a sua expectativa de crescimento do montante disponível para o jogo é a que aposta sempre 25% deste montante. A fim de testar o Critério de Kelly, imagine agora o mesmo jogo, porém que pague R$ 2,00 para cada real apostado (em vez de R$ 3,00). Perceba que este jogo é justo, na medida em que sua expectativa de ganho é zero (você arrisca ganhar ou perder R$ 1,00 com 50% de chances). Neste caso, qual o percentual ideal para se apostar? Na fórmula apresentada, o que mudou foi o parâmetro b, que agora é 2 em vez de 3.
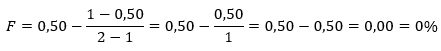
Kelly nos diz para simplesmente não apostar nesse jogo, pois seria perda de tempo ficar jogando inúmeras rodadas para ter expectativa de zero ganho. Perceba que qualquer valor pago acima de R$ 2,00 (para cada real apostado) faria com que a fórmula acima resultasse em um percentual positivo, de modo que quanto maior o benefício (quanto maior b), maior o percentual ótimo F a ser apostado. Por outro lado, caso b seja menor que 2, o jogo teria expectativa negativa e a fração ideal dada pelo Critério de Kelly também seria um percentual negativo, indicando que não vale a pena jogar este jogo (em rigor, o percentual negativo significaria entrar na ponta contrária, caso fosse possível – mas em geral, não é). Por exemplo, para ilustrar, suponha b = 1,50:
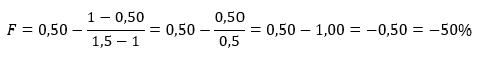
Um outro exercício bacana de se fazer para testar o Critério de Kelly é perceber em que situação a fórmula indicaria uma aposta de 100% (pense antes de seguir abaixo para ver se você consegue antecipar o contexto que levaria a aposta ótima ser de todo o montante disponível). Observe a sequência algébrica a seguir:
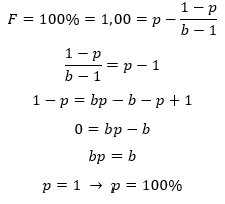
Percebam que o Critério de Kelly passou com louvor no teste, já que ele indica entrar com 100% de todo o capital disponível apenas quando a chance de vitória for de 100%, o que faz total sentido né? Caso haja algum percentual, por menor que seja, de derrota, jamais será razoável apostarmos tudo que temos (100%) em uma rodada, tendo em vista que podemos jogar este jogo inúmeras vezes.
COMO UTILIZAR O CRITÉRIO DE KELLY EM APOSTAS ESPORTIVAS?
O contexto apresentado para validade do Critério de Kelly diz respeito a um jogo que se repete por muitas vezes. Consequentemente, a fórmula apresentada pode ser utilizada para jogadas em série, mas não em paralelo. Ou seja, você precisa definir o montante que você deseja colocar em jogo e qual o jogo “será jogado”. Por exemplo, você pode definir o jogo como sendo apostar na vitória do seu time de coração em todos os seus jogos e quanto você quer disponibilizar para esse jogo. E então bastará aplicar o Critério de Kelly para saber qual o percentual você apostará rodada a rodada. Por exemplo, caso você disponibilize R$ 1.000,00 para o jogo e a fração ideal dada pelo critério de Kelly seja 25%, com b = 3. Note o que pode acontecer:

O Critério de Kelly nada diz se você quiser jogar vários jogos diferentes em paralelo, mas apenas o quanto você deve apostar em cada rodada de um jogo que se repete por diversas vezes. Se você deseja apostar no jogo do seu time por aqui e no jogo do seu time na NBA rodada após rodada, você deverá definir montantes para cada uma das apostas para então poder aplicar o Critério de Kelly separadamente para cada jogo.
CONSEGUIMOS TRANSFORMAR O CRITÉRIO DE KELLY EM UMA ESTRATÉGIA DE INVESTIMENTO?
Se você chegou até aqui neste artigo, ficou claro que o Critério de Kelly não é uma estratégia de investimento, até porque sequer foi concebido no contexto de investimentos. Uma estratégia de investimentos requer não apenas escolher em que ativos devemos investir como que frações do montante a ser investido devem ser alocadas a cada um dos ativos escolhidos. Além disso, o mercado de investimentos não é exatamente um mercado de apostas, né? Há fundamentos por detrás de cada ativo e esses precisam ser considerados. Comprar ações de uma empresa não pode ser interpretado como algo similar a apostar numa roleta de cassino.
Não obstante, muitos pesquisadores e estudiosos levaram o conceito do Critério de Kelly para os investimentos. Mas o resultado foi, de certa forma, frustrante porque, após algumas adaptações, percebeu-se que o Critério de Kelly levava a uma carteira ótima na fronteira de Markowitz. Em outras palavras, utilizar o Critério de Kelly nos investimentos recai sobre um caso específico da teoria de Markowitz.
O grande problema é que esta carteira sugerida pelo Critério de Kelly não considera o apetite de risco do investidor: em qual ponto da fronteira de Markowitz você deseja estar - em uma carteira mais ou menos arriscada? Além disso, o Critério de Kelly usualmente leva a carteiras alavancadas e muitos investidores não podem e/ou não desejam alavancar suas carteiras. No final das contas, o Critério de Kelly nada acrescenta à teoria de carteiras otimizadas; pelo contrário, ele mostra um caminho que pode não ser o ideal - e geralmente não é por não se ajustar ao seu apetite para risco! Além do mais, atualmente já se sabe que a teoria de Markowitz para otimização de carteiras é limitada, até porque foi o primeiro modelo a identificar carteiras otimizadas e, portanto, diante de premissas que podem ser consideradas bastante simples. Já se conhecem estratégias otimizadas que superam aquelas dadas por Markowitz.
Dito tudo isso, não recomendo o uso do Critério de Kelly para formar suas carteiras de investimentos. Eu jamais utilizei pela simples razão de que costumo trabalhar com modelos mais avançados do que Markowitz e, mesmo quando trabalho com este modelo, ele generaliza Kelly de modo que não tenho nenhum tipo de perda ao simplesmente “esquecer” o Critério de Kelly. Ficou claro?
Espero que a leitura tenha sido agradável, didática e que você saia daqui com o Critério de Kelly dominado e desmistificado. É um baita resultado da matemática, útil em determinado contexto, mas não universal. Caso tenha restado qualquer dúvida, te convido a me seguir no Instagram @carlosheitorcampani e no LinkedIn para conversar comigo nessas redes, seja nos meus posts ou mesmo no privado. Deixo um forte e respeitoso abraço a cada um de vocês.
PS: Para quem gosta de apostas esportivas, na minha próxima coluna por aqui (em duas semanas) escreverei sobre algo bacana e importante nesse contexto. Fiquem ligados!
* Carlos Heitor Campani é PhD em Finanças, Certificado pelo CNPI e Pesquisador da ENS – Escola de Negócios e Seguros. Além disso, ele é Diretor Acadêmico da iluminus – Academia de Finanças e Sócio-Fundador da CHC Finance e da Four Capital. Campani pode ser encontrado em www.carlosheitorcampani.com e nas redes sociais: @carlosheitorcampani. Esta coluna sai a cada duas semanas, sempre na quinta-feira.
