‘Tempestade perfeita’ derruba estas ações em mais de 10% hoje; é hora de comprar?
Olá, pessoal. A estrutura a termo de taxas de juros (ETTJ) é um gráfico cartesiano no qual a curva representa determinada taxa de juros em função do prazo (período de tempo para o qual a taxa é válida). Por exemplo, podemos ter uma taxa prevalescente de 13% ao ano para o prazo de 6 meses e uma taxa de 11% ao ano para o prazo de 10 anos. É natural que a taxa de juros mude em função do prazo considerado.
A Anbima (Associação Brasileira das Entidades dos Mercados Financeiro e de Capitais) disponibiliza diariamente duas curvas de juros importantíssimas para o mercado brasileiro: juros nominais e juros reais. Ambas as curvas são baseadas nos títulos do Governo Federal, que em função de um mercado bastante líquido, negocia títulos em juros nominais prefixados (LTN e NTN-F) e títulos em juros reais acima do IPCA (NTN e NTN-B). Tais títulos não consideram todos os vencimentos possíveis, de modo que uma curva matemática se faz necessária para fazer o melhor ajuste possível do que se observa no mercado ao que o modelo teórico prevê.
No caso em tela, o modelo escolhido pela Anbima é o modelo de Svensson (1994). Eu tenho algumas publicações acadêmicas a respeito e quem desejar estudar esse assunto mais a fundo, basta acessar a minha página pessoal (carlosheitorcampani.com) e buscar meus artigos científicos no tema. Aliás, ajudei a construir a metodologia das curvas atualmente utilizadas pela Susep, assunto que fica para outro dia também. No texto de hoje, não quero focar em teorias de curvas de juros. Eu quero falar de um assunto muito pouco debatido e, infelizmente, muitas vezes desconhecido por participantes do mercado. E neste caso, a Anbima embarcou em um erro relacionado a isso.
TAXAS DE JUROS DISCRETAS VS. TAXAS CONTÍNUAS
Quando dizemos que a taxa Selic de mercado é atualmente igual a 13,65% ao ano, estamos lidando com uma taxa em tempo discreto. Por exemplo, para determinar o fator de acumulação de um investimento que rende esta taxa diariamente, fazemos a conta abaixo:
![]()
Isso porque o mercado brasileiro convenciona que há sempre 252 dias úteis em um ano. Desta forma, o fator de acumulação diária e a taxa Selic ao dia são calculados conforme abaixo:
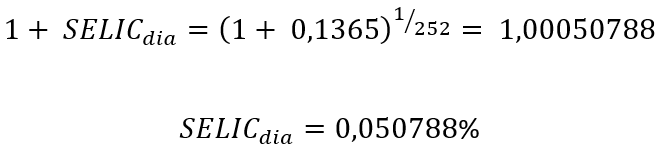
Tanto a taxa Selic ao ano (13,65%) quanto essa mesma taxa expressa ao dia (0,050788%) são taxas discretas e efetivas. O que poucas pessoas sabem é que uma taxa de juros pode ser expressa em tempo contínuo. Uma vez mais, eu não entrarei aqui na origem das taxas contínuas para não tornar este artigo extremamente longo, mas os interessados podem acessar um artigo no qual explico isso em detalhes no meu site ou me solicitando através das minhas redes sociais (@carlosheitorcampani). A matemática que define taxas contínuas e as relaciona com taxas discretas pode ser expressa através do limite abaixo:
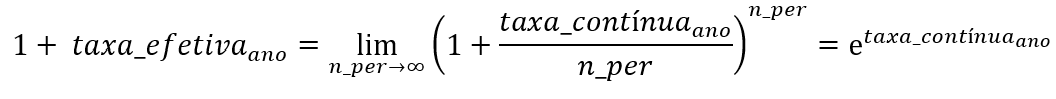
A equação acima nos diz, por exemplo, que uma taxa de 12% ao ano continuamente capitalizada (isto é, uma taxa de 12% ao ano contínua) equivale ao limite acima quando o número de capitalizações (n_per) de uma taxa discreta tende ao infinito. E, neste caso, podemos agora calcular esse limite como:
![]()
Isso equivale a dizer que 12% ao ano continuamente capitalizados corresponde a uma taxa discreta efetiva de 12,75% ao ano. Lidar com taxas contínuas é matematicamente mais simples por conta das propriedades da função exponencial. Via de regra, modelos de juros em tempo contínuo (discreto) preferem taxas contínuas (discretas). Para perceber a facilidade matemática, irei ilustrar um exemplo com uma taxa contínua de 24% ao ano. Quais são os fatores de acumulação para 1 ano, 5 anos, 6 meses e um mês? Cálculos abaixo.

Perceberam como tudo se passa? Basta ajustar linearmente o expoente. Taxas contínuas não são muito utilizadas diretamente no mercado brasileiro, mas, como disse antes, funcionam formidavelmente em modelos contínuos de precificação. Um exemplo relevante onde essas taxas aparecem diz respeito às curvas de juros disponibilizadas diariamente pela Anbima. Muitos não sabem, mas como essas curvas são baseadas em modelos contínuos de juros, elas representam taxas contínuas. Se forem utilizadas na prática, precisam ser transformadas em taxas discretas (fórmula acima) ou a fórmula de valor do dinheiro no tempo precisa ser conforme abaixo:
![]()
E é nesse ponto que a Anbima se confunde em seu site. Observe a tabela abaixo, onde os valores foram fidedignamente retirados do seu site no dia 14 de março, com a curva de fechamento de mercado do dia anterior (segunda-feira).
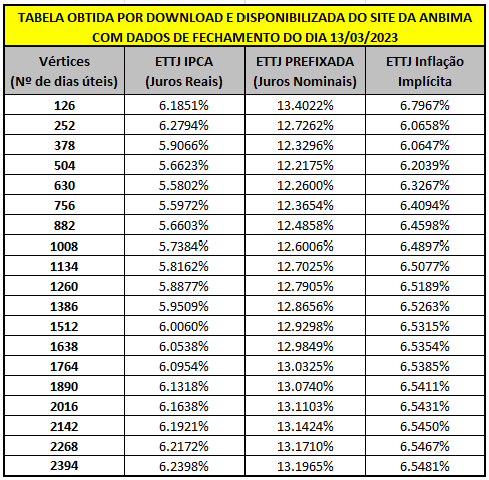
Qual o erro na tabela acima? Observe que a coluna da inflação implícita nasce do chamado efeito Fisher, retirando-se o efeito dos juros reais dos juros nominais. Matematicamente, o efeito Fisher é normalmente apresentado em livros da seguinte forma:
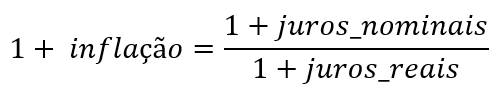
Se você aplicar a fórmula acima às taxas da tabela da Anbima, obterá exatamente a coluna da ETTJ Inflação Implícita. Só que isto está completamente errado. Como as taxas da tabela acima são contínuas, a conta para se chegar à inflação implícita (obviamente, também contínua) seria muito mais simples:
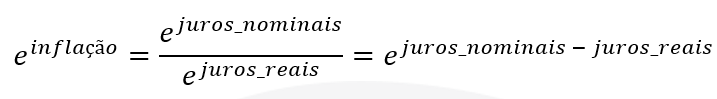
Portanto, concluímos que a inflação implícita em tempo contínuo pode ser obtida simplesmente subtraindo-se os juros reais dos juros nominais. Como disse antes, a matemática das taxas contínuas é bem mais simples! Portanto, esta deveria ser a conta feita pela Anbima, tendo em vista que as taxas de juros estão em tempo contínuo. Uma sugestão seria apresentar todas as taxas em tempo discreto, pois eu tenho segurança em dizer que muitos participantes do mercado acabam usando essas curvas da Anbima como se fossem taxas discretas. E isso, naturalmente, embute um erro desnecessário em seus modelos e cálculos. Para se ter uma ideia da magnitude do erro cometido, abaixo eu recalculei as taxas de juros utilizando a fórmula matemática do modelo de Svensson (para confirmar que as taxas apresentadas pela Anbima eram contínuas). Naturalmente, as taxas bateram, à exceção do truncamento que a Anbima faz em vez de realizar a aproximação correta: note que a quarta casa decimal das taxas são muitas vezes diferentes em uma unidade. Este, aliás, é outro ponto de fácil melhoria que a Anbima precisa implementar: para que truncar quando se pode aproximar de maneira tecnicamente mais correta? Afinal de contas 6,18519% deveria ser aproximado para 6,1851% ou 6,1852%?
Mais à direita da tabela abaixo, calculei as curvas da inflação implícita em tempo contínuo (pela simples diferença das taxas à esquerda) e em tempo discreto (pela fórmula apresentada anteriormente). A última coluna apresenta a diferença entre essas taxas em basis points - bps (unidade muito utilizada no mercado financeira, equivalente a um centésimo de um porcento). Perceba que o erro cometido por quem utiliza a curva de inflação implícita da Anbima é da ordem de 60 bps para baixo, ou seja, o erro induz a pensar que a inflação implícita é 0,60% ao ano menor do que o mercado realmente sugere.
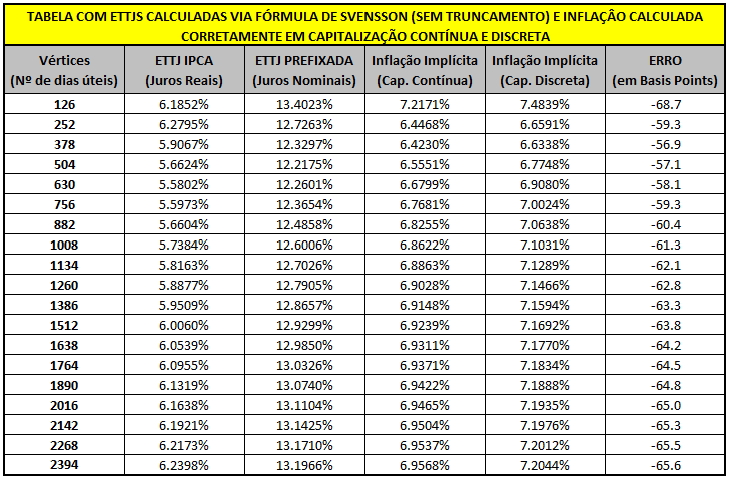
Agora, preciso fazer um disclaimer: tentei algumas vezes avisar a Anbima deste erro, inclusive enviando emails. Infelizmente, nunca fui respondido. Espero que agora este artigo chegue até esta importante instituição, que aliás tem o meu respeito e admiração. Meu objetivo com este texto é compartilhar conhecimento. Quem sabe muitos participantes do mercado não ajustarão seus cálculos de inflação implícita estimada e terão melhores resultados a partir de agora? Este é o meu intuito: colaborar da forma que está ao meu alcance com o mercado e seu desenvolvimento. E o conhecimento é fundamental para isso.
Gostaria de lhe convidar a me seguir no instagram @carlosheitorcampani. Quero tornar essa minha rede social mais forte para atingir mais e mais pessoas com conteúdos relevantes feitos com muito carinho e responsabilidade.
Forte e respeitoso abraço em todos vocês.
* Carlos Heitor Campani é PhD em Finanças, Pesquisador da Cátedra Brasilprev em Previdência e da ENS – Escola de Negócios e Seguros, Diretor Acadêmico da iluminus – Academia de Finanças e sócio-fundador da CHC Treinamento e Consultoria. Ele pode ser encontrado em www.carlosheitorcampani.com e nas redes sociais: @carlosheitorcampani. Esta coluna sai a cada duas semanas, sempre na sexta-feira.
