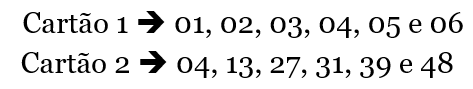Fique por dentro das principais notícias do mercado desta sexta-feira
Olá, pessoal!
Hoje dividirei com vocês três experimentos simples, porém interessantes, que costumo realizar em sala de aula (a depender do curso que estou lecionando, claro) e que ajudam a nos mostrar que, ao contrário do que pensamos, não somos completamente racionais. Mesmo no caso de pessoas com capacidade intelectual acima da média e mesmo pessoas que conhecem a teoria de economia comportamental (e possivelmente leram o célebre livro “Rápido e Devagar, Duas Formas de Pensar”, de Daniel Kahneman), o cérebro, muitas vezes, tenta nos passar a perna. E deixo claro que aqui não estou me restringindo ao sistema 1 (que não é analítico, mas traz respostas rápidas e inconscientes). Estou tratando de decisões irracionais pensadas (de acordo com o sistema 2 de Kahneman), nas quais nosso cérebro teima em desafiar o que sabemos ser conceitualmente correto.
Resolvi escrever sobre este tema porque compreender nossas limitações é um passo importantíssimo para tudo na vida e não seria diferente com nossos investimentos ou mesmo com nossas decisões de consumo e organização financeira pessoal/familiar. Uma decisão não racional nos coloca em desvantagem dentro do contexto dos efeitos daquela decisão e, acima de tudo, traz à tona ineficiências que nos podem custar muito caro a depender do tipo de decisão tomada. Assim como a psicologia ensina alguém com TOC (Transtorno Obsessivo-Compulsivo) a enfrentar as pseudovontades não as realizando, a solução para conter nossa irracionalidade é enfrentar algumas decisões irracionais e mostrar ao nosso cérebro que ele está enganado. Vamos aos exemplos, pois eles (quase) falam por si sós.
-
Qual cartão da Mega-Sena tem a maior chance de ser sorteado?
Talvez esse seja simultaneamente o mais simples e poderoso exemplo do que quero mostrar a vocês. Quando faço essa pergunta, a reação é bastante interessante. A absoluta maioria das pessoas com boa formação em probabilidades compreende que qualquer das duas senas tem rigorosamente a mesma chance no sorteio, mas preferem “por desencargo de consciência”, o cartão 2. Ao questionar os alunos, recebo muitas considerações interessantes (do ponto de vista psicológico), mas muitas delas podem ser resumidas na seguinte frase:
“Professor, os dois cartões acima têm a mesma probabilidade, mas na prática, o cartão não sequenciado tem mais chance de ocorrer”.
Por óbvio, os dois cartões têm a mesmíssima chance de ocorrência. Às vezes, para justificar a escolha do cartão não sequenciado, alguém argumenta que jamais foram sorteados números sequenciados na Mega-Sena. Aqui, claro, tem um erro de argumentação, tendo em vista que o conjunto de cartões não sequenciados tem muito, mas realmente muito mais elementos do que o conjunto de cartões com números sequenciados, levando este segundo conjunto a ter muitíssimo menos chances do que seu concorrente.
Em outras palavras, as pessoas mesmo sabendo da igual probabilidade entre os cartões buscam argumentos não-teóricos para confortar a decisão do cérebro pelo cartão não sequenciado. Para mostrar como isso pode ser ineficiente, faço um jogo onde sortearei aleatoriamente 5 números de 1 a 10. Cada quinteto de números, nesse caso, possui uma chance em 252, pois há 252 quintetos diferentes com os números de 1 a 10. Digo que pagarei a cada R$ 1,00 apostado em um quinteto o montante de R$ 252 (portanto, num jogo de expectativas equilibradas). Mas também digo que pagarei 500 vezes o valor apostado por quintetos sequenciados e mil vezes pelo quinteto de 1 a 5. Mesmo assim, raríssimas são as pessoas que apostam em quintetos sequenciados e mais raras ainda aquelas que apostam no quinteto de 1 a 5. Não obstante, se tomo os 252 dias úteis de um ano comum e pago R$ 1.000 por real apostado no primeiro dia útil do ano, a imensa maioria aposta nesse dia. Entenderam como nosso cérebro trabalhou para nos sabotar no sorteio dos quintetos? E, novamente, reitero que não estamos falando da sabotagem do sistema 1 do nosso cérebro, o que já foi fartamente evidenciado por Kahneman.
-
O Paradoxo de Ellsberg
Pense com bastante calma e responda racionalmente às duas questões abaixo seguir.
Questão #1: Suponha uma urna com 30 bolas vermelhas e outras 60, que podem ser pretas ou amarelas (em qualquer proporção completamente aleatória, não conhecida e a ser sorteada). Escolha uma das apostas abaixo:
![]()
Questão #2: Enunciado idêntico ao anterior - Suponha uma urna com 30 bolas vermelhas e outras 60, que podem ser pretas ou amarelas (em qualquer proporção completamente aleatória, não conhecida e a ser sorteada). Escolha uma das apostas abaixo:
![]()
Aqui o que acontece com a maioria das pessoas é que, mesmo com todo o tempo do mundo para pensar, elas escolhem a aposta A na questão #1 e a aposta D na questão #2. E isso é racionalmente inconsistente. Senão, vejamos.
Primeiro precisamos reconhecer que as apostas concorrentes (A e B; C e D) têm exatamente as mesmas chances de vitória (1/3 na questão #1 e 2/3 na questão #2). Portanto, poderíamos esperar uma divisão mais ou menos meio a meio das pessoas por cada uma das apostas nas duas questões, o que de fato não é observado experimentalmente. Mas, vamos adiante. Ao escolher a aposta A na questão #1, por qualquer razão, a pessoa tem preferência pela cor vermelha em relação à cor preta. Note que a questão #2 acrescenta a bola amarela como também sendo vitoriosa nas duas apostas da questão #1, de modo que novamente a preferência se dá entre as cores vermelha e preta (pois a amarela está em ambas as apostas). Mas ao perceber, na prática, que a maioria das pessoas escolhe a aposta D, trata-se do nosso cérebro mudando sua preferência (da bola vermelha para a bola preta) sem absolutamente nenhuma razão. Isso não é racional.
Claro que nas apostas acima, com chances iguais entre as apostas nas duas questões, a irracionalidade do nosso cérebro não chega a nos fazer mal, mas em outros contextos, o paradoxo de Ellsberg pode sim nos levar a decisões ineficientes. Basta, por exemplo, desequilibrarmos ligeiramente as probabilidades de modo conveniente.
A explicação desse paradoxo se dá porque nosso cérebro odeia o desconhecido. Ao preferir a aposta A, note que sabemos que teremos 1/3 de chances, pois há, de fato, 30 bolas vermelhas na urna. Por mais que nossas chances com a aposta B sejam rigorosamente iguais a 1/3 (pois a divisão entre bolas pretas e amarelas é completamente aleatória), nosso cérebro tende a apostar no que é conhecido contra o que é ambíguo. Já na questão #2, a ambiguidade mudou de lado para a aposta C, tendo em vista que agora sabemos que a urna possui 60 bolas pretas e amarelas (aposta D). Mesmo reconhecendo que tal ambiguidade não impacta nossas chances de vitória, tendemos a preferir o que não é ambíguo e, muitas vezes, pagamos por isso: e então alguém está levando um almoço grátis pra casa às suas custas, perceberam?
-
O Paradoxo de Allais
Tal como no exemplo anterior, escolha uma aposta em cada um dos dois experimentos.
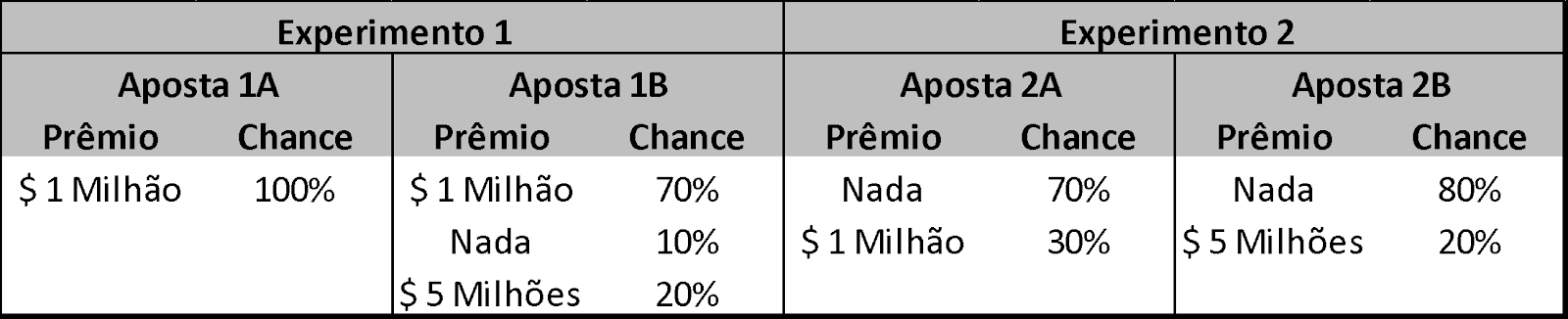
Aqui, a maioria das pessoas escolhe a aposta 1A em vez da 1B, o que é perfeitamente explicável e racional: a aversão ao risco faz com que muitos não queiram arriscar 10% em perder R$ 1 milhão, tendo como contrapartida 20% de chances de ganhar R$ 5 milhões em vez de “apenas” R$ 1 milhão. O problema é que no experimento 2, a maioria das pessoas passa a preferir a aposta 2B em relação à aposta 2A. Se pararmos para analisar, novamente a diferença corresponde a 10% a mais na aposta 2B de nada ganhar contrapondo-se aos mesmos 20% de chances de ganhar R$ 5 milhões. Em tese, as decisões deveriam ser as mesmas.
O que está por detrás disso é que no experimento 1, uma das apostas corresponde à ausência total de risco e, nesse caso, nossa aversão a risco acaba decidindo pala primeira aposta. Já no segundo experimento, como ambas as apostas têm risco, nossa aversão a risco não se revela e acabamos optando pela aposta de maior risco (ou seja, aquela com maiores chances de nada ganhar), mesmo que os ingredientes diferenciais dos dois “lados da balança” sejam exatamente os mesmos que antes. Perceba que o fator “aversão a risco” ora entra em campo, ora fica esquecido.
Em tese, o mesmo racional que nos leva a preferir a aposta 1A deveria nos levar a optar pela 2A, de acordo com toda a base teórica das decisões racionais pela teoria da utilidade econômica. Por esta razão, o paradoxo de Allais se apresenta como um dos maiores desafios a esta teoria, que dá forte base às teorias de racionalidade econômica. Mas essa discussão é bem mais complexa do que quero discutir aqui e daria um novo artigo. Em verdade, o que quero mostrar é que em muitas ocasiões, escondemos nossa aversão a risco e tomamos decisões em prol do risco que normalmente não tomaríamos se o problema fosse apresentado sob outro contexto (mas ainda com os mesmíssimos ingredientes). A solução é sempre pensarmos muito bem no problema para o qual precisamos tomar uma decisão e uma dica é separar os ingredientes diferenciais e analisá-los em outros contextos para termos convicção de que nossa decisão é racional e, portanto, muito bem pensada.
Por hoje é isso pessoal. Esse texto, confesso, me deu enorme prazer em escrever pois este é um assunto que me atrai bastante. Nosso cérebro é, para mim, o órgão mais intrigante do nosso corpo. Compreender melhor como ele responde a situações cotidianas (e aqui falo num contexto muito mais amplo do que apenas em decisões de investimentos ou financeiras) nos faz, em última instância, pessoas melhores e, me arrisco a dizer, muito mais felizes!
Por fim, fica o convite: vamos nos conectar nas redes sociais? Não deixe de me seguir @carlosheitorcampani, notadamente Instagram e LinkedIn. Todo o conteúdo que produzo eu compartilho por lá!
Um forte e respeitoso abraço.
* Carlos Heitor Campani é PhD em Finanças, Professor do Coppead/UFRJ, Pesquisador da Cátedra Brasilprev em Previdência e Pesquisador da ENS – Escola de Negócios e Seguros. Ele pode ser encontrado em www.carlosheitorcampani.com e nas redes sociais: @carlosheitorcampani. Esta coluna sai a cada duas semanas, sempre na sexta-feira.