O paradoxo de Braess, a teoria dos jogos e o desafio de investidores e AAIs

Olá, pessoal! Você já ouviu falar do paradoxo de Braess? O Prof. Dietrich Braess é um matemático alemão com 87 anos que descobriu em 1968 uma situação paradoxal que traz ensinamentos a diversas áreas do conhecimento humano. O paradoxo é construído com base no encadeamento lógico a seguir:

1. É dado um sistema de escolhas com n opções onde cada indivíduo escolhe a sua melhor opção;

2. A esse sistema, acrescenta(m)-se uma ou mais opções de escolha;

3. As opções adicionais podem ser boas ou ruins para os indivíduos;

4. Se forem ruins, a opção anteriormente escolhida se mantém;

5. Se houver pelo menos uma opção melhor, essa é agora escolhida em detrimento da anterior;

6. Em qualquer das situações, o aumento de opções faz com que a nova opção ótima individual seja no mínimo tão boa quanto a anterior (e, em algumas situações, até melhor);

7. Conclui-se, portanto, que ter mais opções não ocasiona perdas em relação à opção ótima original.

Prof. Braess mostrou uma situação paradoxal onde mais opções significa piorar o ótimo individual - se você não acredita, precisa ler este artigo até o final! Dividirei com vocês um exemplo bem fácil, aplicado ao tráfego de automóveis. Imagine que você e diversas outras pessoas queiram viajar da cidade Alfa para a cidade Beta (figura a seguir) e, para isso, existam duas opções de rodovias: uma passando pela cidade X e outra passando pela cidade Y. Os tempos estimados em cada trecho são indicados. Note que da cidade Alfa para a cidade Y e da cidade X para a cidade Beta, o tempo de percurso é constante e igual a 90 minutos porque as rodovias nesses trechos são muito amplas e jamais engarrafam. Já nos outros dois trechos, não tão modernos, o tempo depende do fluxo de carros (dado pela variável N = número de automóveis trafegando pelo trecho). As cidades X e Y, apesar de muito próximas, não têm conexões porque há um rio entre elas que não permite o trânsito de automóveis.

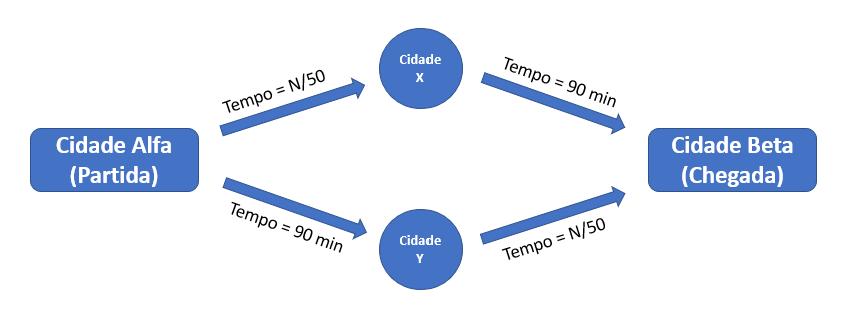
Suponha que o fluxo normal total de Alfa para Beta seja de 4.000 automóveis. Como os caminhos via cidades X ou Y são similares, os motoristas olham aplicativos de trânsito e sempre escolhem o caminho de menor fluxo pois isso minimiza o tempo de viagem. Quando os motoristas fazem isso, a solução ótima se dá com metade do fluxo indo pela cidade X e a outra metade, pela cidade Y. Nesse caso, o tempo total de viagem é minimizado para todos, sendo de 2.000/50 + 90 = 130 minutos. Perceba que qualquer outra divisão dos automóveis pelos percursos levaria um caminho a ser mais veloz que o outro, de forma que os automóveis iniciando o percurso em Alfa o escolheriam, rapidamente reequilibrando o sistema para sua solução ótima. Em teoria dos jogos, esse é um ponto de equilíbrio estável de Nash. É estável porque qualquer desequilíbrio tende a ser rapidamente dissipado. É de Nash porque nenhum motorista tende a preferir outra escolha senão a ótima (porque se o fizesse, aumentaria o fluxo daquele caminho e aumentaria o seu tempo de viagem para além dos 130 minutos).

Agora imaginemos que seja construída uma ponte entre as cidades X e Y, possibilitando o tráfego de automóveis entre essas cidades. Por serem muito próximas, o tempo de mudança entre as cidades X e Y é desprezível e considerado constante e igual a um minuto para os nossos propósitos. A figura abaixo ilustra a nova configuração de trânsito entre a cidades Alfa e Beta. Com essa ponte, uma nova opção para o trajeto, podemos então esperar que o tempo de viagem se reduza ou, na pior hipótese, se mantenha o mesmo? A resposta, paradoxalmente, é não.

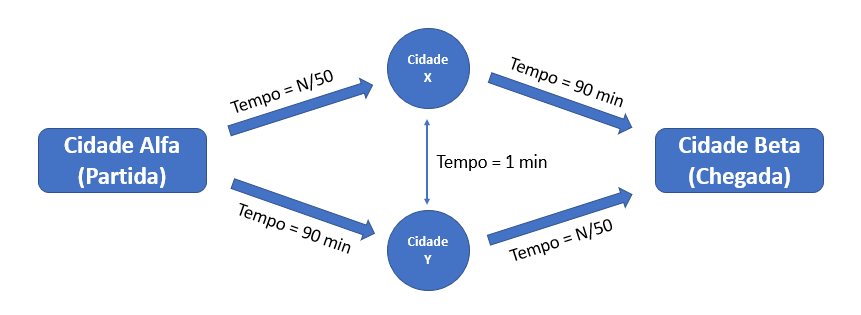
Note que agora cada motorista terá a possibilidade de mudar o percurso da cidade X para a cidade Y. O primeiro a fazer isso teria um tempo de viagem total de 2.000/50 + 1 + 2.001/50 = 81,02 minutos, o que representaria uma redução de quase 49 minutos em relação ao tempo anterior de 130 min. Perceba que ninguém se sentiria estimulado a alterar seu percurso de Y para X porque, nesse caso, o tempo total aumentaria para 90 + 1 + 90 = 181 minutos.

Acontece que mais motoristas pensarão o mesmo e o novo equilíbrio incrivelmente se dá com todos os 4.000 automóveis passando pela cidade X, tomando a ponte para Y e seguindo viagem. O tempo total do percurso aumenta então, de forma extraordinária, para 4.000/50 + 1 + 4.000/50 = 161 minutos. E temos, novamente, um equilíbrio estável de Nash! Nenhum motorista se sente estimulado a viajar por outra rota senão a ótima porque levaria ainda mais tempo (faça as contas por si mesmo!).

O paradoxo de Braess se dá porque com a construção da ponte entre as cidades X e Y, abriu-se uma nova opção de rota (na verdade duas, se considerarmos os dois sentidos), mas o tempo total de percurso aumentou de 130 para 161 minutos.

QUER AGORA ENTENDER A EXPLICAÇÃO?

Lembro que paradoxos são, na verdade, pretensos. Eles parecem destruir a lógica quando, em verdade, essa é indestrutível (desde que bem construída, claro). Os paradoxos servem então para revisarmos a lógica e percebermos qual premissa foi quebrada e, portanto, precisamos revisar. No caso do encadeamento apresentado nos 7 pontos acima, há uma premissa fundamental: que as novas opções não matem, de alguma forma, opções antigas! Essa premissa está implícita especificamente no ponto 4. Pois caso novas opções cancelem a opção ótima anterior, toda a lógica construída cai por terra e a nova opção ótima poderá, sim, ser pior. No exemplo do tráfego acima, ao abrir a ponte, simplesmente a solução ótima anterior ficou inatingível por conta do bom e velho “Dilema do Prisioneiro da Teoria dos Jogos”, lembra dele?

No dilema do prisioneiro, caso os prisioneiros pudessem combinar e um confiar no outro, haveria uma solução ótima global e satisfatória para todos. Mas quando um confia no outro, abre-se espaço para o outro “se dar bem em cima do um” e acaba que ninguém quer ser o “um” e atinge-se o equilíbrio de Nash ruim para todos. No caso acima, é a mesma coisa. Se todos os motoristas continuassem como antes (sem a ponte), o tempo de todos seria os mesmos 130 minutos. Mas aí um motorista perceberia a oportunidade para reduzir seu tempo de viagem a apenas 81,02 minutos. Outros motoristas perceberiam a mesma coisa e... pronto! Todos pagariam o preço e passarão a levar 161 minutos. Isso também carrega outro ponto fortíssimo da Teoria dos Jogos, a chamada “Tragédia dos Comuns” (deixo aqui a curiosidade de cada um aguçar uma pesquisa a respeito).

O exemplo acima pode ser aplicado em diversas outras áreas do conhecimento humano, tais como em eletricidade, em biologia, em liderança de grupos de pessoas e até em estratégias de esporte coletivo como basquete e futebol. Em investimentos, eu também acho que podemos tirar lições. Vamos a isso?

O mercado de investimentos no Brasil vem se desenvolvendo intensamente de uns tempos para cá. Com isso, muitos produtos diferentes estão ao alcance dos investidores. Isso, em tese, é excelente porque aumenta as possibilidades na hora de você formar a sua carteira bem como potencializa os benefícios da diversificação. Entretanto, vejo o perigo de se tratar de muitos produtos diferentes e com isso, um investidor não conseguir ou não querer se esforçar para conhecer todas as alternativas. Consequentemente, ele(a) tende a investir de forma diferente da ótima caso siga sozinho(a). E então, qual a solução que ele(a) tem? Procurar um profissional para auxiliá-lo. E aí entram em cena AAIs (agentes autônomos de investimentos) e, muitas vezes, gerentes bancários. Se esses profissionais não estiverem bem-preparados e conhecerem realmente toda a diversidade de classes atualmente disponíveis para investimento, eles poderão sugerir carteiras enviesadas para aquele tipo de produto que eles mais conhecem (ou prefiram vender). E então, nesse caso e de forma não generalizada, mais opções pode levar a um equilíbrio onde carteiras baseadas em poucos produtos estejam longe da carteira ideal dentro deste mercado e até mesmo dentro de um mercado de poucos produtos, porém dos mais relevantes e efetivos.

Notem que eu não defendo uma simplificação do mercado financeiro brasileiro nem sou contra sua expansão, muito pelo contrário! Apenas reitero a importância desses profissionais terem acesso a uma formação com excelência e muita dedicação para que possam sugerir carteiras realmente otimizadas. No problema ilustrativo do tráfego entre as cidades Alfa e Beta, o problema não foi a construção da ponte em si, pois esta uniu as cidades X e Y e facilitou a vida de seus moradores. O problema gerado pelo novo acesso está em encontrar a solução a fim de coibir a passagem pela ponte de viajantes de Alfa a Beta (como, por exemplo, cobrar um pedágio substancial para não moradores das cidades X e Y). O grande ponto que quero trazer com este artigo é: quando algo se desenvolve rapidamente, ter novas opções é legal, mas ao resolver alguns problemas, pode-se criar outros. É preciso lidar com esses outros e agir da melhor maneira possível.

Espero que vocês tenham gostado! Se você desejar me conhecer melhor e todo o conteúdo que produzo, te convido a me seguir no Instagram @carlosheitorcampani, a acompanhar meu canal no Youtube e a se conectar a mim no LinkedIn. Forte e respeitoso abraço a todos!

* Carlos Heitor Campani é PhD em Finanças, Certificado pelo CNPI e Pesquisador da ENS – Escola de Negócios e Seguros. Além disso, ele é Diretor Acadêmico da iluminus – Academia de Finanças e Sócio-Fundador da CHC Finance e da Four Capital. Campani pode ser encontrado em www.carlosheitorcampani.com e nas redes sociais: @carlosheitorcampani. Esta coluna sai a cada duas semanas, sempre na quinta-feira.