Fique por dentro das principais notícias do mercado desta segunda-feira
Na coluna anterior, iniciei a discussão sobre a precificação dos títulos públicos, com foco nos títulos pré-fixados. Hoje, voltaremos nossa atenção ao Tesouro Selic (LFT), título indexado à taxa Selic. Ao final desta coluna, o objetivo é que você, investidor, esteja apto a calcular o preço justo de qualquer LFT, em qualquer data. A rentabilidade da LFT acompanha a variação da taxa Selic, calculada desde a data de liquidação da compra até o vencimento, acrescida do ágio ou deságio aplicado no momento da aquisição. Esses ajustes, determinados pela demanda de mercado, influenciam diretamente o preço de compra ou venda do título. No site do Tesouro Direto, o deságio é indicado por um sinal positivo, o que significa que o investidor paga um valor mais baixo pelo título e, consequentemente, obtém uma rentabilidade maior. O contrário ocorre no caso de ágio, quando o título é adquirido por um preço superior, reduzindo o retorno.
É fundamental lembrar que a precificação da LFT ocorre por marcação a mercado. Mas qual a diferença em relação à marcação na curva? Na marcação na curva, o valor do título é calculado de forma teórica, baseado na taxa contratada no início da operação (t0) e permanece constante, sendo menos suscetível às oscilações da curva de juros. Já na marcação a mercado, a precificação é ajustada conforme a taxa de juros vigente, o que torna o preço do título mais volátil. No caso das LFTs, o spread (ágio/deságio) não tem sido significativo nos últimos meses, o que minimiza a diferença entre a marcação a mercado e a marcação na curva. Para exemplificar, nos últimos 12 meses, o deságio variou pouco, com um intervalo entre 0,14% e 0,17%, o que impactou de forma limitada o preço desses títulos.
Entretanto, é importante destacar que, embora a volatilidade dessa taxa tenha sido baixa nos últimos 12 meses, isso não garante que o cenário se repetirá no futuro e perdas podem, de fato, ocorrer. Essas perdas, provavelmente, não serão tão significativas quanto as observadas em uma NTN-B (tema da próxima coluna), mas é crucial que o investidor mantenha a marcação a mercado como prioridade, evitando surpresas indesejadas. A título de exemplo, a LFT 2029 registrou um retorno negativo de -0,03% em um único dia no ano passado (02/05/2023). O leitor pode argumentar que esse valor foi irrelevante e eu concordo. No entanto, se a variação do deságio fosse mais acentuada, a rentabilidade poderia ter sido ainda menor. Mesmo assim, certamente não se compararia à volatilidade de títulos pré-fixados, como a LTN ou a NTN-F, ou de títulos atrelados à inflação, como a NTN-B.
Acredito que ao falarmos da precificação, esse ponto ficará ainda mais claro. A seguir, listo as etapas de cálculo:
-
Cálculo do Valor Nominal Atualizado (VNA): foi instituído o valor nominal de R$ 1.000 em uma data-base (01/07/2000), que servirá de referência para atualização do valor nominal. Sendo assim, VNA = 1.000 x (1 + Selic Acumulada entre o dia 01/07/2000 e a data da compra). O fator 1+Selic Acumulada entre duas datas pode ser encontrado no site do Banco Central.
-
Como a liquidação ocorre 1 dia após a compra, não há o valor da Selic diária, portanto, é necessário utilizar a Meta Selic vigente. Sendo assim, calcula-se o VNA projetado para o dia da liquidação como:
![]()
-
A inclusão do ágio ou deságio é refletida na chamada “Cotação”, onde:
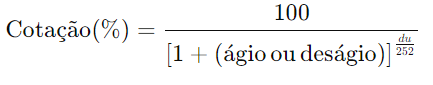
Vamos agora calcular o preço da LFT com vencimento em 01/03/2029 disponível no site do Tesouro Direto em 25/09/24 e compará-lo com o valor calculado pela fórmula no Excel. O deságio utilizado de 0,1394% foi extraído do próprio site, conforme mostrado na figura retirada do Tesouro. O prazo é determinado pelo número de dias úteis entre a data de liquidação (D+1 em relação à data de compra) e a data de vencimento (exclusivo). Os feriados podem ser encontrados no site da Anbima, com informações disponíveis até 2099. No Excel, a função para calcular o número de dias úteis é a DIATRABALHOTOTAL (data_inicial; data_final - 1; [feriados]). Nesse caso, a data inicial será a data de liquidação, que no exemplo é 26/09/2024 (D+1, onde D é o dia da compra), e a data final será 01/03/2029, de acordo com o vencimento da LFT. O ajuste "-1" na fórmula exclui a data de vencimento do cálculo.
O fator da Selic Acumulada encontrado no link citado anteriormente é mostrado a seguir:

Ao calcular o preço da LFT usando a fórmula, é importante lembrar que a base de cálculo é de 252 dias úteis por ano. Portanto, o fator de tempo n é igual a 1106/252. Na tabela abaixo, verifica-se os valores encontrados do VNA, VNA projetado, Cotação e Preço da LFT 2029.
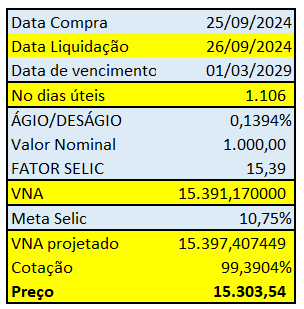
Abaixo, o print do site do Tesouro para a mesma LFT.

Antes de concluir, é importante destacar a relevância da marcação a mercado, mesmo no caso da LFT, que costuma ter uma volatilidade de preço menor em comparação com outros títulos. Para ilustrar esse ponto, farei uma simulação comparando o preço na curva e a mercado ao longo de 5 dias, variando o deságio durante o período. Utilizarei a Meta Selic para projetar o Valor Nominal Atualizado (VNA) nos dias subsequentes, já que a Selic diária não está disponível. Observa-se que, nesse intervalo, ocorreram dois retornos diários negativos, ambos resultantes do aumento no deságio.

Caro leitor, conforme mencionado anteriormente, na próxima coluna falarei sobre a precificação dos títulos indexados ao IPCA. Como de costume, caso tenha ficado alguma dúvida em relação ao assunto, fico à disposição por e-mail. Até a próxima!
