Brasil rejeita alegações dos EUA e diz não reconhecer legitimidade do USTR para investigar práticas comerciais do país
Hoje compartilharei com vocês o problema de Monty Hall, assim conhecido porque ficou famoso ao ser apresentado por Monty Hall em seu programa “Let´s Make a Deal” (algo como o Silvio Santos e o seu “Porta da Esperança”: aqui apenas os mais velhos entenderão – risos!). O jogo começa com três portas fechadas, onde em apenas uma delas há um belo prêmio, tal como um carro luxuoso (e nas outras, há bodes que você não gostaria de levar para casa no lugar do carraço). O apresentador do programa, obviamente, sabe em que porta se esconde o grande prêmio.
O jogo é composto sempre pelas seguintes etapas:
-
Monty Hall pede que você se posicione em uma das portas, numeradas de 1 a 3;
-
Monty Hall abre uma das outras duas portas (necessariamente) com um bode;
-
Agora restam apenas a porta que você escolheu e uma outra fechadas e, claro, se sabe que uma delas esconde o carro;
-
Monty Hall lhe pergunta se você deseja trocar para a outra porta fechada ou permanecer na que você previamente escolheu;
-
Você decide-se por manter ou trocar a porta;
-
Monty Hall abre todas as portas, mostrando atrás de qual está o carro: se for a sua porta, você ganha o carrão!
E aí, você troca de porta no passo 5 acima ou mantém-se fiel à sua escolha inicial?
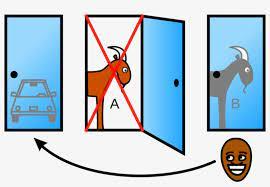
A questão ficou famosa porque a maioria absoluta achou (acha!) que trocar de porta é irrelevante quando, em verdade, não é! Você deve trocar se quiser aumentar as chances de acertar a porta com o carro bacana.
Muitos pensam, equivocadamente, que ao sobrarem duas portas, as chances são 50/50%, o que está errado. O conceito por detrás do problema é o de probabilidade condicional. O problema de Monty Hall não se equivale a oferecer duas portas e pedir para você escolher uma delas. Ele é condicionado à sequência de etapas que enumerei acima e o ponto-chave é que o apresentador sabe onde está o carro e ele sempre abrirá uma porta com bode.
Há diversas formas diferentes que eu poderia usar para explicar que, ao trocar de porta, você sobe de 1/3 (um terço) para 2/3 (dois terços) as suas chances de acertar onde está o carro. Darei uma explicação técnica e um exemplo mais claro para convencer aqueles que estão incrédulos.
Ao fazer sua escolha inicial, acho que ninguém discutirá que a probabilidade de acerto é de 1/3 porque há uma porta com o carro num total de três portas. Como o apresentador SEMPRE poderá abrir uma OUTRA porta com um bode, essa nova informação NÃO altera a probabilidade inicial de 1/3 por se tratar de algo que NÃO depende da sua decisão inicial.
Por outro lado, ao escolher inicialmente qualquer porta, sua chance de encontrar um bode é de 2/3, que se dividiam entre duas portas, de forma que cada uma delas possuía 1/3 de chances de esconder um belo carro. Quando Monty Hall abre uma das portas com bode, ele simplesmente torna a probabilidade dessa porta igual a ZERO (certeza de não haver um carro ali). Mas a probabilidade total das duas portas não escolhidas não se alterou e continua 2/3, de modo que agora a nova informação (porta aberta com bode) altera as probabilidades nessas duas portas: uma passa a ser de zero e a outra, portanto, concentra toda a probabilidade de 2/3! Assim, ao mudar, você dobra de um para dois terços as suas chances.
Se você ainda está confuso, vamos fazer uma outra brincadeira com EXATAMENTE a mesma ideia e contexto do problema de Monty Hall. Suponha que você ganhará uma bolada de dinheiro se acertar o dia do mês no qual eu nasci. Bom, há 31 dias possíveis, de 1 a 31. Você provavelmente não escolheria 29, 30 ou 31 por estes dias não aparecerem em todos os meses e, portanto, carregarem menos probabilidades. Suponha que você escolha qualquer dia como, por exemplo, o dia 10.
Fazendo analogia com o jogo das portas, há 31 portas fechadas e você escolheu a de número 10. Nesse momento, eu abro todas as portas exceto a sua (número/dia 10) e outra, a de número 24 (que eu escolho deixar fechada). Note que em todas as que eu abri, há um bode porque eu não posso abrir a porta com o grande prêmio, ou seja, eu não posso dizer ainda nesta etapa em que dia eu nasci. Agora eu te dou a oportunidade de mudar de porta: você está no dia 10 e eu já te dei a informação de que eu não nasci nos dias 1, 2, ..., 9, 11, 12, ..., 22, 23, 25, 26, ..., 31. Só há duas alternativas para o dia em que eu nasci: a que você inicialmente escolheu (dia 10) e a do dia 24. Você troca o dia 10 pelo dia 24?
Ficou fácil agora né? Por que será que eu deixei exatamente a porta do dia 24? Nesse caso, porque eu realmente nasci no dia 24! Ao mudar de porta, você está apostando que você errou inicialmente ao escolher a porta 10. Como essa escolha foi aleatória e a chance de você ter errado é enorme (aproximadamente 30 em 31, desprezando a questão inicialmente abordada de que os dias 29, 30 e 31 têm menos chances de serem escolhidos). Desta forma, ao mudar para a porta do dia 24, suas chances de vencer no jogo aumentam consideravelmente. Qual a única chance de você PERDER o jogo ao trocar de porta? Caso eu tivesse realmente nascido no dia 10, mas essa chance já sabemos ser muito pequena por conta do número muito maior de “outras portas”.
Caso você ainda queira se convencer, entre em qualquer ferramenta de buscas online e procure pela simulação do jogo de Monty Hall. Há diversos sites legais. Ao simular o jogo muitas vezes, experimente sempre trocar de portas e você perceberá que encontrará o carro, aproximadamente, a cada duas de três tentativas. Se você experimentar a estratégia de nunca trocar de porta, irá perceber que vencerá em cerca de um terço das vezes.
E o que esse jogo tem a ver com estratégias de investimento? Ora, ele demonstra um aspecto comportamental que pode ser mais ou menos forte em você, mas certamente existe: o apego que temos às nossas decisões passadas. Temos forte tendência de querer “mostrar ao mundo que estávamos certos”. Muitos investidores se confundem e acham que uma mudança em sua estratégia significa dizer que sua estratégia foi inicialmente errada. Não é disso que estou falando. Ao escolher qualquer porta, não há uma delas com menos chances do que as outras (ou seja, não há estratégia errada propriamente dita). Entretanto, com a nova informação de Monty Hall, uma nota estratégia se torna mais eficiente (ou seja, com mais chances de vitória) e, nesse caso, mudar sua estratégia (i.e., mudar de porta) de modo algum torna sua decisão inicial equivocada.
Com o passar do tempo, as condições do mercado podem se alterar significativamente, de modo a fazer uma estratégia diferente da atual ser mais adequada para você. Há simplesmente uma miríade de fatores que não controlamos, dentre os quais alguns totalmente imprevisíveis (tal como saber que porta Monty Hall abrirá após eu escolher a minha!). Desta forma, eis a dica que prometi no título deste artigo:
“O fato de mudarmos uma decisão passada (como, por exemplo, a nossa estratégia de investimento) não necessariamente indica que essa decisão (ou seja, a estratégia inicial) foi equivocada: novas informações, novos contextos ou novos objetivos podem fazer com que a melhor decisão (estratégia) no passado não seja a melhor no presente. Mudar, nesse caso, é inteligente e não podemos permitir que o viés comportamental do apego a decisões passadas prejudique o bom discernimento e a melhor tomada de decisão.”
Pessoal, espero que tenham gostado: fico à disposição em minhas redes sociais (notadamente no Instagram e no LinkedIn) @carlosheitorcampani. Ah, e não deixem de comentar abaixo o que acharam. Muito obrigado sempre.
* Carlos Heitor Campani é PhD em Finanças, Pesquisador da Cátedra Brasilprev em Previdência e da ENS – Escola de Negócios e Seguros, Diretor Acadêmico da iluminus – Academia de Finanças e Sócio-Fundador da CHC Treinamento e Consultoria. Ele pode ser encontrado em www.carlosheitorcampani.com e nas redes sociais: @carlosheitorcampani. Esta coluna sai a cada duas semanas, sempre na quinta-feira.
